Simetri Lipat dan Simetri Putar
Simetri Lipat dan Simetri Putar. Simetri Lipat adalah
jumlah lipatan yang dapat dibentuk oleh suatu bidang datar menjadi 2
bagian yang sama besar. Untuk mencari simetri lipat dari suatu bangun
datar maka dapat dilakukan dengan membuat percobaan dengan membuat
potongan kertar yang ukurannya mirip dengan yang akan diuji coba.
Lipat-lipat kertas tersebut untuk menjadi dua bagian sama besar. Jika
suatu bangun dilipat menjadi dua, sehingga lipatan yang satu dapat
menutup bagian yang lain dengan tepat, maka dikatakan bangun tersebut
memiliki simetri lipat.
Simetri Putar adalah jumlah putaran yang dapat dilakukan terhadap suatu bangun datar di
mana hasil putarannya akan membentuk pola yang sama sebelum diputar,
namun bukan kembali ke posisi awal. Suatu bangun mempunyai simetri putar
jika ada satu titik pusat dan bangun tersebut dapat diputar kurang dari
satu putaran penuh sehingga bayangannya tepat pada bangun semula.
Percobaan dapat dilakukan mirip dengan percobaan pada simetri lipat
namun caranya adalah dengan memutar kertas yang telah dibentuk. Jika
suatu bangun datar diputar melalui pusatnya dan dapat tepat menempati
tempat semula maka dikatakan bangun tersebut memiliki simetri putar.
Banyaknya bangun tersebut menempati tempat semula dalam sekali putaran
menjukkan jumlah simetri putar. Arah perputaran mengikuti arah jarum
jam.
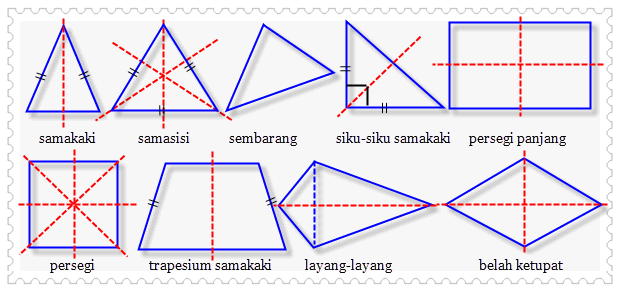
Sumbu simetri adalah garis yang membagi suatu bangun menjadi dua bagian sama besar. Berikut ini sumbu simetri dari beberapa bangun datar
Berikut ini simetri lipat, simetri putar dan sumbu simetri beberapa bangun datar :
| No | Nama Bangun Datar | Simetri Lipat | Simetri Putar | Sumbu Simetri |
| 1 | 1 | - | 1 | |
| 2 |
Segitiga samasisi
| 3 | 3 | 3 |
| 3 |
Segitiga sembarang
| - | - | - |
| 4 |
Segitiga siku-siku samakaki
| 1 | - | 1 |
| 5 | 2 | 2 | 2 | |
| 6 |
Persegi
| 4 | 4 | 4 |
| 7 | - | 2 | - | |
| 8 | 1 | - | 1 | |
| 9 |
Trapesium siku-siku
| - | - | - |
| 10 |
Trapesium sembarang
| - | - | - |
| 11 | 1 | - | 1 | |
| 12 | 2 | 2 | 2 | |
| 13 | tak terhingga | tak terhingga | tak terhingga | |
| 14 |
Oval/Elips
| 2 | 2 | 2 |
| 15 |
Segienam Beraturan
| 6 | 6 | 6 |
Catatan : Bangun datar dikatakan tidak mempunyai simetri putar jika hanya dapat diputar satu keliling lingkaran penuh atau satu putaran. Contohnya : segitiga samakaki, segitiga siku-siku sama kaki, trapesium samakaki, dan layang-layang.
- Segitiga sama sisi mempunyai 3 simetri putar dengan sudut putar 120°, 240°, dan 360°.
- Persegipanjang mempunyai 2 simetri,putar dengan sudut putar 180° dan 360°.
- Persegi mempunyai 4 simetri putar dengan sudut putar 90°, 180°, 270°, dan 360°.
- Belah ketupat mempunyai 2 simetri putar dengan sudut putar 180° dan 360°.



Untuk oiii
BalasHapus